ZAGADNIENIA BADAWCZE
Grupa badawcza Modelowania i Symulacji numerycznych składa się z kilkunastu osób zajmujących się różnymi zagadnieniami badawczymi jak: stabilnością materiałów (kompozytów, elastomerów, tkanek biologicznych), propagacją fal w ośrodkach ciągłych, dynamiką pojazdów i optymalizacją. Ponadto rozwijamy szereg metod symulacyjnych jak: Local Interaction Simulation Approach (LISA), perydynamika oraz metody wieloskalowe.
Biomechanika tkanek miękkich
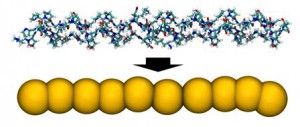 Tworzenie modelu CG tropokolagenu Tworzenie modelu CG tropokolagenu |
W ramach badań nad materiałami kolagenowymi, skupiamy się na zjawisku stabilności oraz degradacji włókien kolagenowych. W trakcie badań używamy metod eksperymentalnych oraz takich metod modelowania jak Dynamika Molekularna, Grubo-Ziarnista Dynamika Molekularna CG-MD, SPH, Metoda Elementów Skończonych itd. Wyniki naszych prac mogą być interesujące zarówno dla inżynierów biomedycznych jak i dla osób badających stabilność biokompozytów kolagenowych. |
Prace nad tym zagadnieniem koordynuje dr hab. inż. Andrzej Młyniec.
Termomechaniczna stabilność materiałów polimerowych oraz kompozytów
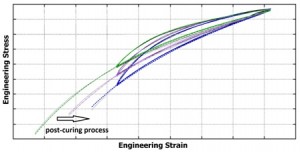
Wpływ procesu sieciowania na lepkosprężytość
|
Długoterminowe właściwości statyczne i dynamiczne materiałów polimerowych zależą od wielu czynników środowiskowych m.in.: wilgotności, temperatury, obciążenia itd. Czynniki te zmieniają właściwości lepkosprężyste materiału, modyfikując tym samym odpowiedź dynamiczną struktury. Do badania tych zjawisk używamy zarówno metod eksperymentalnych jak i modelowania chemomechanicznego. Jeżeli jesteś zainteresowany wynikami naszych prac dotyczących tworzyw sztucznych i kompozytów to zapraszamy do sekcji „Publikacje” |
Prace nad tym zagadnieniem koordynuje dr hab. inż. Andrzej Młyniec.
Propagacja fal sprężystych w ciałach stałych
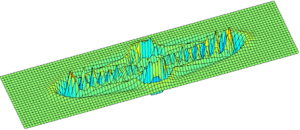 |
Prace badawcze dotyczą modelowania zjawiska propagacji fal sprężystych w ciałach stałych. W pracach badane są własności różnych technik dyskretyzacji pod kątem możliwości redukcji wpływu dyspersji numerycznej na wyniki symulacji. Jedną z analizowanych metod jest Metoda Różnic Skończonych w sformułowaniu nielokalnym do dyskretyzacji przestrzennej. Sformułowanie nielokalne umożliwia efektywne modelowanie ośrodków stałych niedyspersyjnych bez uciążliwej konieczności nadmiernego zagęszczania siatki dyskretnych stopni swobody modeli numerycznych. |
Prace nad tym zagadnieniem koordynuje dr inż. Adam Martowicz.
Nielokalna dyskretyzacja dla kontinuum mechanicznego – perydynamika
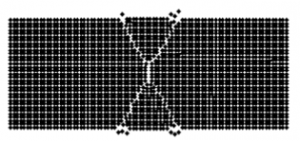
Propagacja pęknięcia w dwuwymiarowym modelu analizowana przy pomocy perydynamiki
|
Perydynamika stanowi stosunkowo nowe podejście w modelowaniu własności ciał stałych (brył odkształcalnych). Matematyczne podstawy perydynamiki bazują na całkowym sformułowaniu równania ruchu, zamiast na równaniach różniczkowych cząstkowych, jak to ma miejsce w przypadku metod klasycznych. W związku z tym nieliniowości geometryczne, np pęknięcie, mogą być znacznie łatwiej wprowadzane do modeli bez ryzyka numerycznej niestabilności algorytmów obliczeniowych. Nielokalne sformułowanie perydynamiki pozwala również na modelowanie spontanicznego rozwoju zaistniałego uszkodzenia. |
Prace nad tym zagadnieniem koordynuje dr inż. Adam Martowicz.
Metody numeryczne do analizy niepewności
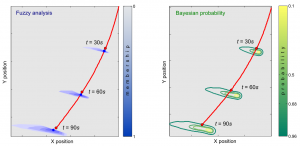
Uncertain position of a rover travelling on soft soil
|
Analiza niepewności w symulacji komputerowej dotyczy metod numerycznych które mogą być stosowane do uwzględniania niepewności różnej natury mogących pojawić się w trakcie modelowania systemu fizycznego. Niepewności mogą być w parametrach modelu lub w sformułowaniu modelu. Różne metody jak np. probabilisticzna lub posybilistyczna mogą być stosowane aby uwzględnić efekt niepewności w sposób najbardziej skuteczny. |
Prace nad tym zagadnieniem koordynuje dr inż. Alberto Gallina.