RESEARCH TOPICS

The Numerical Simulation and Modeling group comprises several researchers, concerned with the investigation of different phenomena, including stability of polymeric materials (composites, elastomers, biological tissues), wave propagation in solids, vehicle dynamics and optimization. Moreover, we develope a number of simulation methods like: LISA for computational mechanics, peridynamics and other multiscale methods.

Biomechanics of soft tissues

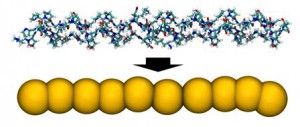Development of CG model of tropocollagen

Our research is dedicated to understanding stability of collagen-based materials through experimental investigations and computational multiscale modeling. We use several different modeling techniques like: Molecular Dynamics, Coarse-Grained MD, Smooth Particle Hydrodynamics, Finite Element Modeling etc. The results of our studies can be interesting for both biomedical engineers and engineers working on the issue of stability of collagen-based biocomposites.

The research is coordinated by Dr Andrzej Mlyniec.

 Thermomechanical stability of polymeric materials and composites

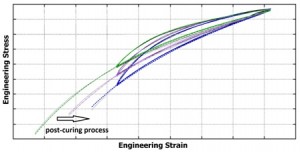
Influence of the post-curing process on viscoelasticity

Long term static and dynamic behavior of polymeric materials depends on several environmental factors e.g. humidity, temperature, external loading etc. These factors alter viscoelastic properties of polymers which result in modified dynamic response. We use experimental and chemomechanical modeling methods. If you are interested in our works regarding polymer and composite stability, please go to the section “Publications”

The works are carried out under the supervision of Dr Andrzej Mlyniec.

Wave propagation in solids

The research deals with modeling the phenomenon of propagation of elastic waves in solids. Various discretization techniques are considered to reduce the influence of numerical dispersion on the results. Finite Difference schemes in a nonlocal formulation are investigated for spatial discretization as promising numerical tool for modeling a nondispersive media with reasonable requirements regarding mesh density.

The research is coordinated by Dr Adam Martowicz.

Nonlocal discretization for mechanical continuum – peridynamics

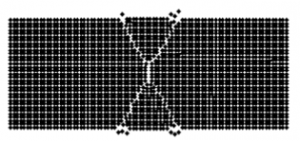
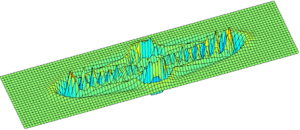
Damage propagation in a 2D model carried with peridynamics

The peridynamics offers a novel approach in computational mechanics for modeling solids. The mathematical foundation of the method is based on the integral based formulation of equation of motion, instead of partial differential equations, as present in classical approaches. Hence, geometrical nonlinearities, e.g. notches, may by introduced into a model much more easily without a risk of numerical instability. A nonlocal formulation in the peridynamic allows for simulations of spontaneous damage propagation.

The research is coordinated by Dr Adam Martowicz.

Numerical methods for uncertainty analysis

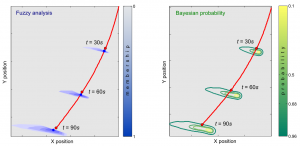
Uncertain position of a rover travelling on soft soil

Very accurate computer models may have limited utility when applied to a process subjected to significant uncertainty. Indeed, computer models yield deterministic outcomes which are in contrast with responses of real processes always affected by some level of uncertainty. Uncertainty analysis aims at including in the modeling and simulation phases existing lack of knowledge on the process under study. This produces more reliable predictions. Many procedures have been developed in the literature for addressing the issue in an effective and efficient manner.

The research is coordinated by Dr Alberto Gallina.